“Science is a way of thinking much more than it is a body of knowledge”.  Said by Carl Sagan

There are many real-life stories of Archimedes. One story rises above all; it goes like this – when he was asked by King to determine if his newly purchased golden crown had any silver added by the goldsmith. A few days later, the greatest scientist found the answer while taking bath, and he was so excited he ran to the street naked, shouting aloud Eureka (I found it).

Alas, this great man was killed by Roman soldier mistakenly while he was carrying a mathematical instrument as he was trying to surrender to Roman. The Roman soldier thought it was a valuable item to steal. Surely, it had no value to the soldier, but a valuable item for humanity, indeed. His contribution to humanity played a big role for all ancient, modern and quantum scientists and physicists.

Spin:

My write-ups on this subject are for all audiences including all young adult with limited knowledge of physics. In case of complexity for any section, please ignore the section. There are so many materials in public domain that you can expand your knowledge on the subject without any limit.

Let us understand what ‘spin’ is? An electron has various intrinsic properties, e.g. electric charge, spin, and mass. Before we discuss ‘spin’ we would like to review some classical mechanics.

Modern Scientists have determined from their observation and calculation that there are 4 fundamental forces of nature.

Electromagnetism,
Gravitation,
Strong interaction and
Weak interaction.

All these forces have an influence on the motion of the elementary particle. Concept of spin is very important for understanding nature in microscale.  Modern scientists, physicists, and quantum physics use spin in mathematics from the energy point of view in building elements as we can see in the periodic table. In this article, we will also discuss nuclear shell in a nutshell.

Torque:

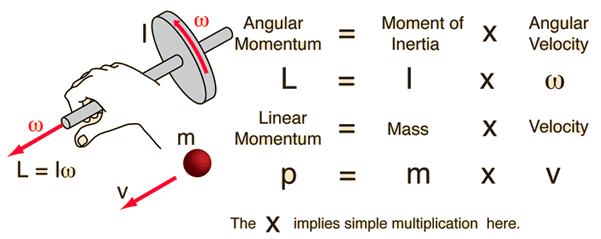
We can envision linear force (F) as a quantity for push or a pull. Similarly, torque can be thought of as a twist to an object. So torque or moment of force is viewed as a rotational aspect of the motion. Let us denote it as capital M (moment of force)

Moment of Inertia:

In physics “The moment of inertia” (say angular mass or rotational inertia)  a quantity that determines the torque needed for a desired rotational angular acceleration; just as the force needed for the desired acceleration of a mass.

Conservation of momentum:

Conservation of linear momentum means the product of mass and velocity must remain constant.

Conservation of angular momentum means the product of ‘moment of inertia and angular velocity’ must remain constant

In both classical and quantum systems, angular momentum, linear momentum, and energy are three fundamental properties of motion.

Since we are discussing Spin property our stress will be angular momentum.
There are several angular momentum operators:
Total angular momentum (denoted by Capital J),
Orbital angular momentum (denoted by Capital L), and

Courtesy of Google

These equations are good both in classical and quantum mechanics.
Quantum mechanics deals with fundamental particles, whereas Classical mechanics deals matter in macroscopic scale.

Quantum mechanics calculate discrete values of energy, momentum, angular momentum and consider all objects with characteristics of both particles and waves (wave-particle duality); and calculation precision guided by statics with (uncertainty principle).

L = r x p; r is position operator; p is a quantum operator which equals to particle mass momentum at each point of rotation.
Spin angular momentum (spin is denoted Capital S).

‘Spin’ is an intrinsic form of angular momentum carried by elementary particles, and atomic nuclei. Spin in quantum mechanics refers to angular momentum, orbital angular momentum which is analogous to the classical angular momentum of orbital revolution.

In 1922 the existence of spin angular momentum is discovered from experiments, such as the Stern–Gerlach experiment. All elementary particles of a given kind have the same magnitude of spin angular momentum, which is indicated by assigning the particle a spin quantum number.

Even though the spin unit is classical angular momentum type but in practice, spin is given as a dimensionless “spin quantum number” by dividing the spin angular momentum by the reduced Planck constant ħ.

Does particle literally spinning? NO

NO.Spin does not mean particle literally spinning. All elementary particles have a characteristic spin. For example, electrons always have “spin 1/2” while photons have “spin 1”
Spin means the number of rotations required by a particle to regain its original stable state and “look” exactly “same” from an excited state.
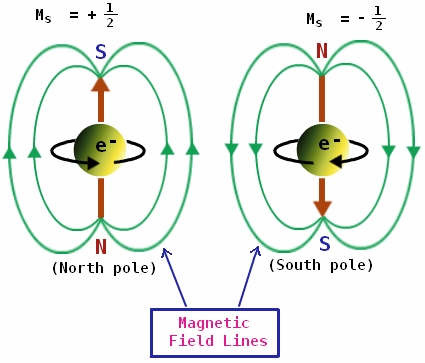
Electron is a quantum particle. The electron spin direction has an influence on magnetic properties of the atom.

Courtesy of Google

The electron can spin in two directions:

1. Spin up
2. Spin down

These spins (spin up and spin down) are the particles which have spin s equal to 1/2, for electrons.

Spin means the number of rotations required by a particle to regain its original stable state and “look” exactly “same” from an excited state.

A book on a table needs a complete rotation of 360° until it looks again the same. So it is “Spin-1” behavior: You must have noticed after half a rotation (180°) playing card looks same; like spin-2.

All electrons have 1/2 spin. A spin-1/2 particle needs two full turns (2×360°=720°).

So it seems rotation of 360° changes to the negative state from a stable state; a further rotation of 360° takes it to the original state. Physicists proved this behavior experimentally and mathematically.

All matter in the universe is built from fundamental particles having 1/2 spin, such as electrons, quarks, muon, tao, etc. These are called “Fermions”.

A particle having 1 spin (integral spin) such as photons, gluons, gravitons, All these fundamental particles are subject of particle physics. You will find a few principal guides us to particle physics.

One of them is “Pauli’s Exclusion Principle”. It says certain particles cannot be at the same place at the same time, with the same energy.

Due to the uncertainty principle, quantum statistics played the main role for calculation. It states that the more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa.

‘Fermions’ particles obey the Fermi-Dirac statistics. Pauli principle applies only to particles with half-integral spin.

The other is called “Bose-Einstein condensate”. Integral spin (1 spin) particles obey Bose-Einstein statistics and are called ‘Bosons’. The particles of integral spin are allowed to go all into the same state. Satyendra Nath Bose proved this principle for photons (spin 1) in 1920, and this principle was adopted by Albert Einstein in 1924 to generalize for all integral spin particles. Particles with integral spin are named after Bose.

Bose-Einstein condensate can be thought of as the fifth states of matter. Other states are Gases, liquids, solids, and plasmas. Bose-Einstein condensates weren’t created in the laboratory before the 1990s.

Nature always wants to bring everything to its minimum energy level for stability. Similarly, all fundamental particle will try to stay at a minimum energy level for stability.

Nuclear shell:

The nuclear shell model of the atomic nucleus uses the “Pauli exclusion principle” to describe the structure of the nucleus in terms of energy levels.

Atomic shell model describes the arrangement of electrons in an atom. Filled shell results in greater stability. Nuclear shell is somewhat analogous to this idea.

It is found that nuclei with even numbers of protons and neutrons are more stable than those with odd numbers. Following are the magic number “magic numbers” of neutrons and protons.

2, 8, 20, 28, 50, 82, 126

The nucleus is tightly packed. In an atom, electron space is 1800 times more than nucleus space. We may expect proton and neutron are constantly colliding, but it is not true. Stability comes due to the above magic number.

This stability suggests that it does not behave like an electronic shell structure. Scientist determines nucleon moves in an effective potential well/box.

Total angular momentum of a nucleus is denoted by I (nuclear spin).

Simple harmonic motion:

We all know from our early mechanics and physics about mass-spring harmonic oscillator and simple harmonic motion. Quantum physics due to extreme micro nature extends this classical idea in analysis of energy waveform. It is rather complex, so, for now, we accept nuclear spin in the conservation of momentum.

Courtesy of Google

Please stay tuned for more about nuclear shell and momentum.