Topic Mass Energy Concept

“Common sense is the collection of prejudices acquired by age eighteen.” – Albert Einstein
“It will seem difficult at first, but everything is difficult at first.” -Miyamoto

In1865, Maxwell (13 June 1831 – 5 November 1879) demonstrated that electric and magnetic fields travel through space as waves moving at the speed of light.

Oliver Heaviside (18 May 1850 – 3 February 1925) calculated effective mass as m = (4⁄3) E / c2, where E is the energy of the sphere’s electric field. Other Physicists got the same result; named as “electromagnetic mass” of the electron a charged sphere.

Henri Poincaré (29 April 1854 – 17 July 1912) considered conservation of momentum of charge and magnetic field. Then Poynting’s theorem predicted that the field acts as a “fictitious fluid” with mass such that E = mc2.

J. J. Thomson (18 December 1856 – 30 August 1940), in 1881 calculated the magnetic field by a moving charged sphere, a most fundamental form of an object, showing that field energy in turn induced a mass into the sphere itself. The field of the sphere acts as a resistance to the charge, so the effective mass of the sphere was induced by the magnetic field.

Fritz Hasenöhrl (30 November 1874 – 7 October 1915) in 1904 experimented with heat energy and concluded that blackbody radiation has mass m = (4⁄3) E / c2.

The modern concept of Mass–energy equivalence defined by Einstein that the equivalence of mass and energy is a consequence of spacetime. WOW! Does the inertia of a body depend on its energy content? In 1905, he described mass equivalence of energy as m = E/c2. Notice the term velocity of the light is the part of the equation, to understand this relationship we need to review special relativity.

The additional energy from the moving particle has contributed the inertia to the particle, and this in turn suggests that all of the particle’s inertia (from its rest mass m and induced mass from movement of the particle) corresponds to some form of energy.

Einstein thereby equates the mass of an object with its total energy content “E = mc2 “as the short punch line to a long and winding scientific story.

Einstein explained this relationship by employing the relativistic principle (the relativistic Doppler shift)

Special relativity:
Einstein postulates
1. Laws of physics are the same for all observers. (Even our simple mind can fully agree with this)
2. The speed of the light is the same for all observers. (But this looks like a trick, relativity solves it)
Let us go back the time when Galileo’s (February 15, 1564 – January 8, 1642) inquisition was due to support for Copernicus (19 February 1473 – 24 May 1543). Galilean relativity states that the laws of motion are the same in all inertial frames (observers in its own frame are either at rest or moving at a constant velocity, not accelerating). A person in the boiler room under the deck does not know if the ship is moving, but a person outside on the deck feels the ship is moving as he sees relative to the shore. These are the relativity and different frame of reference conceptually. However, physics demands concept must be proved by mathematics and here great physicists and mathematicians come for rescue. Galilean transformation says objects velocities add together, space and time don’t depend on velocity. Newton’s view of ‘space and time’ is two separate entities and absolute.

Based on Lorentz transformations Einstein altered the relativity from the Newtonian view of space-time. Modern science implied space and time are connected by light into ‘Spacetime’. This began modern and quantum science in a different footing from Newtonian time. Now we know spacetime is the reality and independent of all observers. Nature and physics had never changed but our mathematics and perception have altered forever.
Newton’s theory versus special relativity
A comparison can be made between Newtonian relativity and special relativity.
Some of the assumptions and properties of Newton’s theory are:
1. Time is absolute.
2. Frame reference uses simple Galilean transformation.
Special relativity follows:
1. The relative velocities between two inertial frames are connected by the speed of light.
2. No universal time, each inertial frame possesses its own notion of time.
3. Frame reference uses Lorentz transformations.
Ole Roemer (25 September 1644 – 19 September 1710) from astronomical observation determined light speed is finite and calculated the speed with known mathematics of that time. The power of mathematics had continually improved for accuracy.
Hippolyte Fizeau (23 September 1819 – 18 September 1896) gave a better measurement of light. One of the first precise calculations of light’s velocity was made in the 1920s by Albert Michelson.
Named after Hendrik Lorentz (18 July 1853 – 4 February 1928) Lorentz transformations are used for a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. Lorentz and others explained mathematically how the speed of light was observed to be independent of the reference frame and applied to the laws of electromagnetism. The Lorentz factor or Lorentz term is the factor used for calculation of time, length, and relativistic mass for an object while that object is moving in relation to the speed of light.
After Maxwell’s equation, a lot of experiments and mathematical research proved time dilation and object length contraction as conjecture. Space-time came in the picture with special geometry (Minkowski Space-Time) for an explanation. Einstein’s special relativity along with Lorentz transform became an accepted principle in modern physics.
A flashlight and a mirror can explain the effect of relativity. The speed of the light is the same for all observers; the moving observer (sitting inside the train) does not know the path of the light travels for the stationary observer outside the train. You and I know it takes a longer path for the stationary observer (outside the train). A simple calculation can be derived by using a triangle. For an outside observer, light travels along the two sides of the triangle whereas for inside observer light path is from the vertex of the triangle straight down to the base of the triangle. This effect raises concepts of time dilation and length contraction which is solved by using the Lorenza factor.
Is e=mc2 true in all cases? No! The mass of an object increases with its velocity. Sometimes it is referred to as relativistic mass. It is useful in mass-energy relations at the subatomic particle level. Not true for our every day’s mass. Two concepts are important in this discussion-inertia and momentum. Inertia is a property of matter which resists the change of motion. A small object can move easier than a large object. At low speed, it appears the effect of inertia has some form of proportionality to the mass of the object. But for a high-speed effect of mass and inertia is not equivalent.
Momentum in physics is very similar to every day’s term, higher momentum is hard to stop. A small object like a bullet with high speed can’t be stopped easily due to its large momentum. We are familiar with the momentum equation. p = mv. This equation is nicely applicable to all speeds in our normal daily life. A high-speed train can’t be stopped easily due to its high momentum. But it is not applicable for extremely high speed that we encounter in subatomic particles.
Extreme high speed the momentum equation should be written as p=γ mv. At 10% of the speed of light, γ is 1.005 and at 50% of the speed of light, γ is 1.155. So in real life γ is 1. But for photon or subatomic particles, we must consider γ.

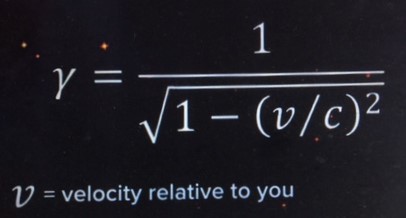
Lorenzo factor

(From Google)
Similarly, energy should be written as e= γ * mc2; m is the rest mass, Gamma comes from the relativistic mass. This equation is only applicable when an object has mass and moving not at the speed of light,
When v = 0; e=mc2 is correct. The object is not moving with respect to you. When an object starts moving faster and faster relative to the speed of the light, energy increases, but not mass.
There is another equation that works with both mass and massless.
When a particle is in motion, its momentum (p) needs to be considered in an energy equation. In 1928, Paul Dirac extended Einstein’s mass-energy equivalence equation (e=mc2) and considered the effect of motion. The complete form of the energy-momentum relation equation is e2 = (mc2)2 + (pc)2. When the mass isn’t considered such as a massless photon or gluon, the energy is simply momentum times the speed of light (e=pc).
e2= (pc)2 + (mc2)2 ; this works with mass or no mass.
If p (momentum) = 0; e=mc2 is true.
So you see mass is not needed for energy, also momentum has a serious relationship with energy.
If we consider mc2 is the energy at rest, so the physical implication of gamma is:
λ = Total energy of a particle while moving /energy of a particle at rest.
Symmetry: Most important example of symmetry in physics is that the speed of light has the same value in all frames of reference,
Key Notes:
The speed of Causality can be defined as the speed limit of cause and effect, it has a maximum value. Lorentz transformation (LT) works with the Maxwell equation in all reference frames. Einstein realized how spacetime is interconnected using LT over Newtonian/Galilean transformation. It predicts the speed of causality. But it requires a constant speed of light, which is also speed of electricity and magnetism. LT proves the reality in all frames. Relativity, symmetry, and consistency are satisfied by LT. The constant factor c in LT has a limit to make all experiments successful in all reference frames. There must be a cosmic speed limit. It is the maximum speed for two objects to talk to each other. Any observer can see this event. It is the reality and math work perfectly. The very existence of mass; and space tells us the limit is finite, infinity is not reality.
Based on LT Einstein derived SR, time dilation, length contraction, spacetime and equivalency of mass/energy, etc.